Johnson graph

Johnson graph
The Johnson graph J(5,2)
Named after	Selmer M. Johnson
Vertices	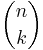$\binom{n}{k}$
Edges	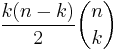$\frac{k (n - k)}{2} \binom{n}{k}$
Diameter	$min(k, n - k)$
Properties	( $k (n - k)$ )-regular Vertex-transitive Distance-regular
Notation	$J (n, k)$

Johnson graphs are a special class of graphs used in several branches of mathematics and computer science. The vertices are the $k$ -element subsets of an $n$ -element set. Two vertices are adjacent when they meet in a $(k - 1)$ -element set. Johnson graphs are denoted by $J (n, k)$ .

The Johnson graph $J (n, k)$ closely related to the Johnson scheme, an association scheme in which each pair of $k$ -element sets is associated with a number, half the size of the symmetric difference of the two sets. The Johnson graph has an edge for every pair of sets at distance one in the association scheme, and the distances in the association scheme are exactly the shortest path distances in the Johnson graph.

Both Johnson graphs and the Johnson scheme are named after Selmer M. Johnson.

Special Cases

$J (n,1)$ is the complete graph $K n$ .
$J (4,2)$ is the octahedral graph.
$J (5,2)$ is the complement graph of the Petersen graph. More generally, for all $n$ , the Johnson graph $J (n,2)$ is the complement of the Kneser graph $KG (n,2)$ .

References

Weisstein, Eric W.. "Johnson Graph". From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/JohnsonGraph.html.
Brouwer, Andries E.. "Johnson graphs". http://www.win.tue.nl/~aeb/graphs/Johnson.html.